Heißluftballons bauen

Kleine, formschöne, flugfähige Heißluftballons kann man selbst bauen.
Anleitung und Hinweise zum Bau und Betrieb von Modellheißluftballons
|
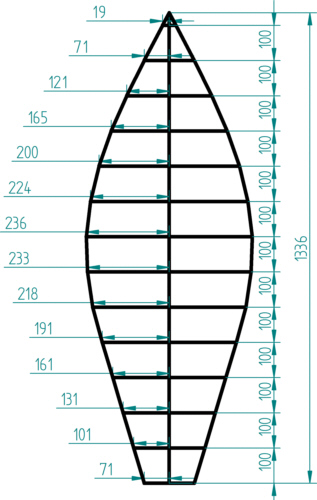
Hier wird der Bau eines Heißluftballons beschrieben, der eine Höhe von 115 cm hat. Das ist eine praktische Größe: noch handlich mit wenig Material zu bauen und zu starten, aber schon groß genug, damit er auch gut fliegt (Ballonfahrer würden sagen "fährt"). Wenn Sie einen Ballon anderer Größe bauen möchten, können Sie die hier angegebenen Maße entsprechend skalieren. Falls Sie einen Ballon mit einer anderen Form bauen möchten, steht Ihnen eine Datei zur Berechnung anderer Ballonformen zur Verfügung. Benötigtes Material und Werkzeug
|
|
Arbeitsschritte
- Auf einem steifen Blatt Papier (mindestens 120 g/m2) mit einer Breite von 472 mm und einer Länge von 1336 mm zeichnen Sie das obenstehende Schnittmuster auf und schneiden es aus. Die Maßangaben sind in Millimetern. Dieses Blatt kann natürlich auch aus mehreren kleineren Stücken zusammengeklebt werden.
- Kleben Sie je zwei Seidenpapierbögen (die haben meist 50 cm x 70 cm und wiegen etwa 18 g/m2) an der Schmalseite mit Klebestift zusammen. Das Papier überlappt dabei 15 bis 20 mm.
- Zeichnen Sie die sechs Papierbögen für den Ballon (evtl. zusammengeklebt) einzeln oder jeweils einige übereinander gelegt (man kann sie mit Stecknadeln zusammenheften, damit sie nicht gegeneinander verrutschen) mit dem Schnittmuster an.
- Schneiden SIe die Bögen einzeln oder wenige Bögen zugleich so zu, dass an allen Seiten 15 bis 20 mm Rand außerhalb der gezeichneten Linie bleiben zum Kleben der Bögen.
- Je zwei Bögen von der Spitze her mit Klebestift am Rand einstreichen und aneinander kleben. Ein Bogen liegt dabei am Boden, der andere wird hochgehalten, damit er nicht versehentlich an der falschen Stelle verfrüht mit dem anderen verklebt. Wenn man immer etwa 40 cm der Kante mit Klebstoff bestreicht, dann 35 cm der Kante verklebt, dann wieder 40 cm mit Klebstoff einstreicht usw., dann reduziert sich das Risiko, dass etwas ungewollt verklebt. Wichtig ist, dass keine Löcher bleiben, durch die später die warme Luft entweichen würde. Die letzte Bahn ist die schwierigste, da man sie nur mit einer Hand im Ballon an die andere Bahn kleben kann.
- Unten an der Ballonöffnung einen ausreichend stabilen Pappring (etwa 30 mm hoch und 90 cm lang, aus 300 g/m2–Papier) an den Ballonrand kleben, um die Öffnung aufzuhalten. Das Ende des Streifens doppelt legen, sonst reißt der Ballon an der Stelle ein.
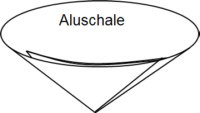
- Eine kleine Schale (etwa 100 mm Durchmesser) aus dicker Alufolie formen. Am einfachsten trichterförmig, wobei die Wand dann an einer Seite doppelt liegt (siehe Skizze oben). Alternativ kann man eine leichte Getränkedose aus Aluminium oben abschneiden, seitlich mit etwas größeren Zuluftlöchern versehen und oben am Rand Löcher zur Befestigung bohren.
- Die Schale mit drei dünnen Drähten an dem Pappring befestigen (durchstechen!). Die Drähte so lang machen, dass die Schale etwa 10 cm unter der Unterkante des Ballons hängt.
Start des Ballons
Formal ist vor dem Aufstieg von Heißluftballonen – sogenannten „Fluglaternen“ – eine Freigabe nach §16a LuftVO erforderlich. Der Antrag soll zwei Wochen im Voraus bei der Deutschen Flugsicherung online gestellt werden. Das örtlich zuständige Ordnungsamt erteilt Auskünfte zu regionalen Regelungen. Der Wikipedia-Artikel zu Kong-Ming-Laternen gibt Hinweise zu regionalen Regelungen. Der Autor dieses Textes übernimmt natürlich keinerlei Verantwortung für jedwede Folgen oder Schäden, die aus dem Bau oder dem Betrieb eines Heißluftballons entstehen.
Den Ballon bei kaltem Wetter und nur, wenn keine Waldbrandgefahr besteht, in einem Abstand von über 20 m von Häusern oder Bäumen (sonst bleibt der Ballon eventuell hängen) starten. Es muss fast windstill sein für einen erfolgreichen Start, sonst drückt der Wind den Ballon zusammen und die warme Luft wieder heraus. Man braucht für den Start am besten vier Personen. Zwei halten den Ballon. Ein dritter heizt den Ballon am besten mit einer Lötlampe (gibt es mit Gaskartusche in Baumärkten) vor (die Aluminiumschale ist dabei leer!). Wenn sich der Ballon aufbläht und schon abheben will, wird die Lötlampe entfernt und ausgestellt. Der vierte hat in sicherem Abstand einen Wattebausch (oder drei Abschminkbäuschchen) mit wenigen Kubikzentimetern Brennspiritus getränkt. Diese Watte legt er in die Schale (die Lötlampe ist aus!) und zündet ihn mit einem Feuerzeug an (am besten so eines mit langer Spitze zum Kerzen anzünden). Alternativ kann man auch Trockenbrennstoffe wie Grillanzünder verwenden, was beim Start sicherer ist. Dafür verlöscht dieser nicht von selbst, sollte der Ballon abstürzten. Der Spiritus erreicht den Boden nur aus sehr geringer Höhe noch brennend. Wenn der Ballon nach oben zieht, lassen beiden Haltenden zugleich los, damit der Ballon nicht kippt. Geht der Ballon beim Start in Flammen auf: Abstand halten und nicht zu löschen versuchen! Jetzt braucht man Fahrräder, will man dem Ballon folgen. Der Brenner verlöscht nach wenigen Minuten, der Ballon fliegt – auch bei fast windstillem Wetter – oft mehrere Kilometer weit.
Wenn Sie einen Ballon nach dieser Anleitung gebaut haben, würde ich mich über eine Rückmeldung freuen (Emailadresse steht im Impressum).
Anmerkungen:
|
|
Dieser Heißluftballon war ein Versuch, einen besonders leichten Ballon aus Haushaltsfrischhaltefolie zu bauen. Diese Folie wiegt nur 10 g/m2 und ist schwer zu verarbeiten. Um sie überhaupt verarbeiten zu können, wurden vor dem Verkleben feine Balsaholzkreuze auf die einzelnen Folien geklebt. Der Ballon war etwa 50 cm hoch und hatte ein geringes Volumen. Für einen mitfahrenden Brenner war er zu klein. Nach dem Aufheizen mit einer Lötlampe stieg der Ballon schnell zur Zimmerdecke, verweilte dort wenige Sekunden und sank dann sehr schnell herab. Das kleine Volumen verliert – auch über Wärmestrahlung – sehr schnell an Wärme. Große Heißluftballons tragen also nicht nur größere Lasten, weil ihr Gesamtvolumen größer ist. Ihr 'Oberfläche-zu-Volumen'-Verhältnis ist auch kleiner, was sowohl den Gewichtsanteil der Hülle am Gesamtgewicht reduziert, als auch die Wärmeabstrahlung reduziert. Einen Ballon zu bauen, der deutlich kleiner als ein Meter ist und mit Brenner fliegen soll, ist schwierig. |
Faltenbälge herstellen
Faltenbälge werden zum Beispiel verwendet, um ein Objektiv mit einer Kamera zu verbinden oder um bewegliche Maschinenteile zu gehäusen. Der Faltenbalg dient dabei dem Schutz des Inneren vor Schmutz, Gasen oder Licht aus dem Außenraum oder dem Schutz der Umwelt vor beweglichen Teilen oder Chemikalien im Innern des Faltenbalgs. Faltenbälge können unterschiedlichste Querschnitte und Längen haben und aus verschiedenen Materialien gefertigt sein. Hier wird erläutert, wie man Faltenbälge aus zähem Papier oder leichtem Karton herstellen kann, die für den Einsatz an Kameras oder in einem Balgengerät geeignet sind. Die hier beschriebenen Faltenbälge sind aus einem einzigen Bogen Papier gefertigt. Natürlich ist es möglich, Faltenbälge aus vielen Einzelstücken zusammen zu kleben oder zu nähen, was andere Faltengeometrien ermöglicht. Faltenbälge aus gummiartigen Kunststoffen können in fast beliebiger Form gefertigt werden.
Es empfiehlt sich, einen Vorversuch mit einfachem Papier zu machen, ehe man sich an die Fertigung eines langen Faltenbalgs aus teurerem Material macht. Die erste Abbildung zeigt einen halbfertigen Faltenbalg aus dünnem, festem Papier.
Faltenbälge mit quadratischem Querschnitt

Als erstes wird die Herstellung eines Faltenbalgs mit konstantem quadratischem Querschnitt beschrieben. Dazu wird eine Zeichnung angefertigt, die den korrekten Papierzuschnitt ermöglicht:
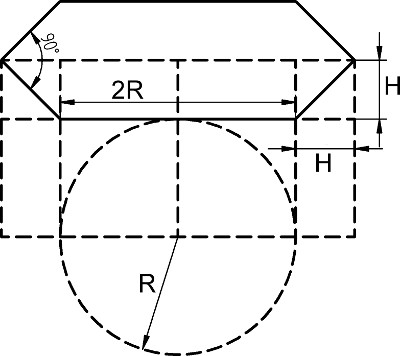
Der Faltenbalg in diesem Beispiel soll später einen quadratischen Querschnitt mit der Kantenlänge 2R freihalten. Nach der Skizze oben wird das mit der durchgezogenen Linie begrenzte Sechseck konstruiert. Die Höhe H bestimmt das maximale Außenmaß 2R+2H des Faltenbalgs. Ein großes H führt dazu, dass man für eine vorgegebene Länge des Faltenbalgs weniger Falten braucht, ergibt aber ein großes Außenmaß. Da mehr Falten auch mehr Arbeit bedeuten, ist eine Höhe H mit etwa 10 bis 20 mm meist gut gewählt. Man kann sich auch am Querschnitt orientieren und etwa H=R/2 oder H=R/3 wählen.
Im nächsten Schritt wird dieses Rechteck wie in der nächsten Skizze vervielfältigt und das Muster auf das Papier übertragen, aus dem der Faltenbalg entstehen soll:
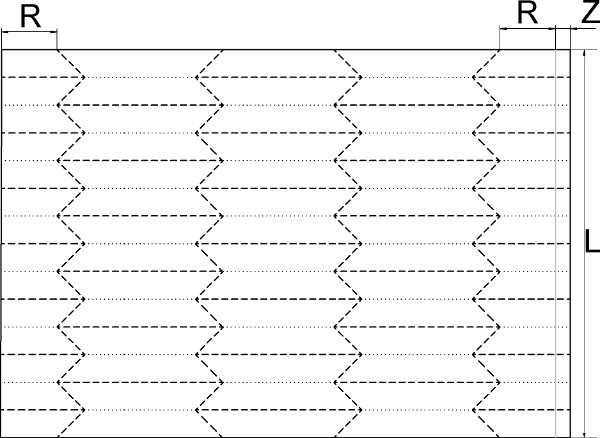
Wenn der Faltenbalg ausgezogen eine maximale Gesamtlänge G haben soll, ergibt sich die Papierlänge L zu mindestens L=2G. Das Papier wird beim Ausziehen in den Knicken weniger belastet, wenn eine größere Länge, zum Beispiel L=2,5G gewählt wird. Die minimale Gesamtlänge des zusammengepressten Faltenbalgs liegt mindestens bei 1,2*Papierdicke*2*L/H, also etwa bei 5*Papierdicke*G/H. Das Maß Z gibt den Klebeüberlapp an. Dieser sollte je nach Fertigungsgenauigkeit bei 5 bis 10 mm liegen. In dieser Skizze stehen gestrichelte Linien für Kanten, die beim fertigen Faltenbalg nach außen gefaltet werden. Punktierte Linien stehen für Kanten, die später nach innen gefaltet werden. Alle Linien werden mit Lineal und Falzbein genau vorgerillt. Anschließend wird das Blatt zu einem Rohr gerollt und die beiden Kanten werden um die Länge Z überlappend verklebt. Dann werden an einem Ende des Rohrs beginnend die Falten eine nach der anderen von Hand gefaltet. Die ersten Falten sind schwieriger, danach wird es einfacher.
Soll der Faltenbalg innen einen rechteckigen Querschnitt von 2R·B haben, wechseln sich im Zuschnitt entsprechend lange und kurze Sechsecke ab:
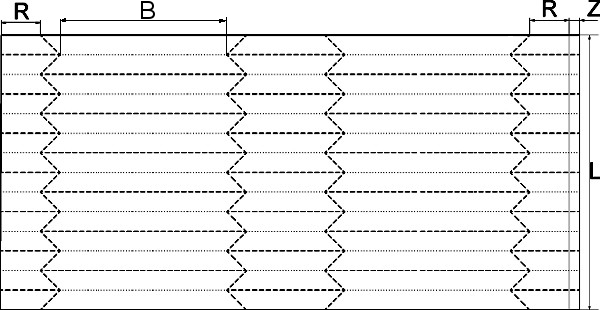
Faltenbälge mit sechseckigem Querschnitt
Soll der Faltenbalg keinen rechteckigen, sondern beispielsweise einen sechseckigen Querschnitt erhalten, so ändert sich in der ersten Grundzeichnung der Winkel α von 90° auf 120°. Der Winkel α berechnet sich zu α=180°-360°/N, mit der Zähligkeit N=6 für einen sechseckigen Querschnitt. Faltenbalgen mit einem ungeraden N sind so nicht möglich, da beim Verkleben des Zuschnitts eine Falte nach innen auf einer Falte nach außen zu liegen kommt. Man kann dies durch ein versetztes Verkleben ausgleichen und erhält dann einen schraubenförmigen Faltenbalg, der sich nur begrenzt zusammenschieben lässt, wobei sich die beiden Enden gegeneinander verdrehen.

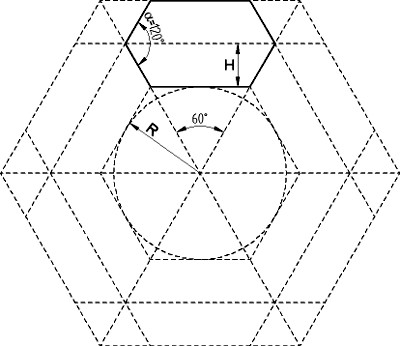
Konische Faltenbälge
Soll der Faltenbalg an den beiden Enden einen unterschiedlichen Querschnitt haben, so wird die Zeichnung für den Papierzuschnitt komplizierter. Die Höhe H verringert sich dabei vom weiteren zum engeren Ende des Faltenbalgs. Als Beispiel soll ein sechseckiger Faltenbalg konstruiert werden, welcher der Übersichtlichkeit halber nur wenige Falten hat.

Als erstes werden zwei Kreise gezeichnet mit den Radien Ri und Ra, wobei Ri der halbe Innendurchmesser auf der engeren Seite des Faltenbalgs ist und Ra der Radius auf der weiten Seite des Faltenbalgs. Diese Kreise werden wie in der Zeichnung in 30°-Schritten (also 360°/2/N) geteilt und eine waagerechte Tangente wird an den kleineren Kreis gezeichnet:
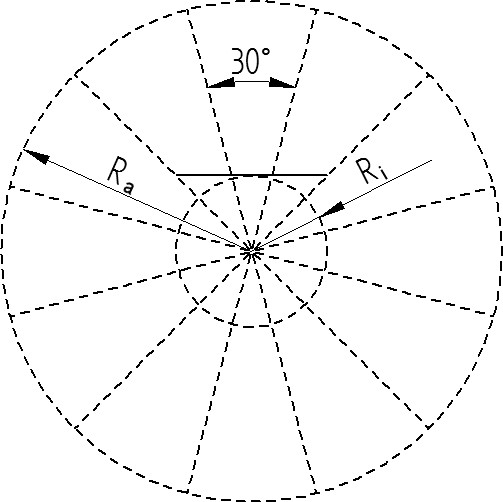
Als nächstes werden weitere Linien entsprechend der folgenden Zeichnung eingezeichnet, bis die gewünschte Anzahl Falten beziehungsweise der äußere Durchmesser erreicht ist:
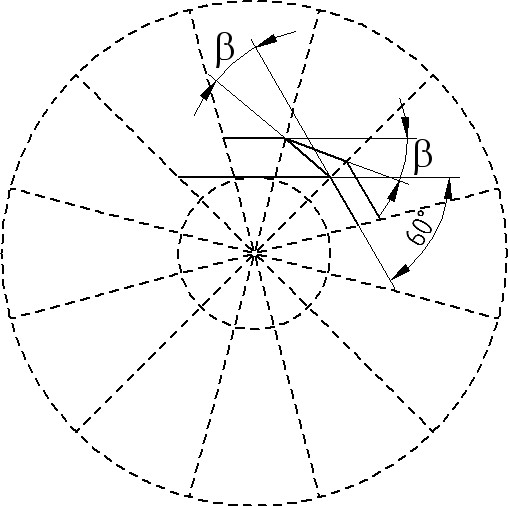
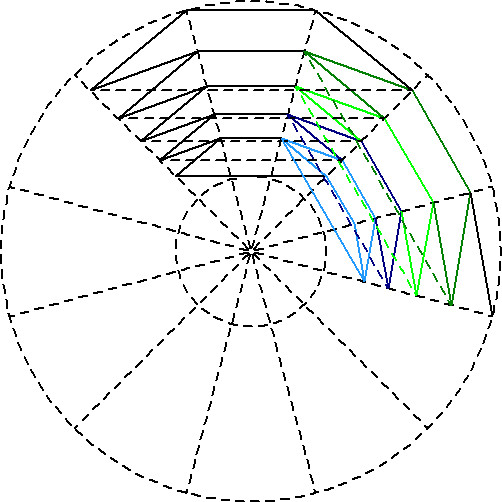
Der 60°-Winkel wird als 360°/N (hier: N=6) gewählt. Von der Wahl des Winkels β hängt ab, wie viele Falten der Faltenbalg zwischen den beiden Enden hat. Dieser Winkel β bestimmt damit auch die maximale Gesamtlänge des Faltenbalgs. Welches der richtige Winkel β ist, wird weiter unten berechnet, da die Berechnung einleuchtender ist, wenn man die Konstruktion schon verstanden hat. Die Konstruktion der Linien wird bis zum äußeren Kreis analog fortgeführt, wobei es Linien in genau vier Richtungen gibt, die jeweils zueinander parallel sind:
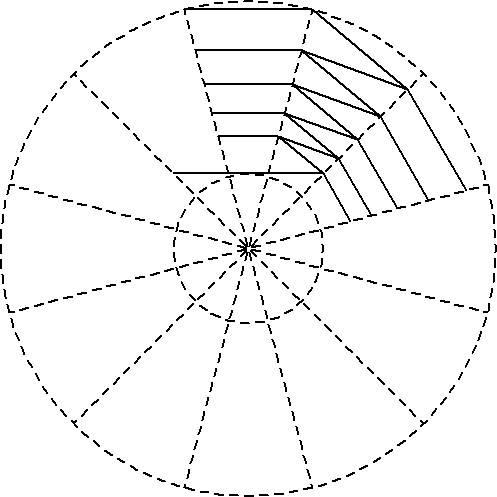
Durch Spiegelung an zwei Hilfslinien (hier rosa gezeichnet) wird die schräge Zickzacklinie zweimal kopiert:
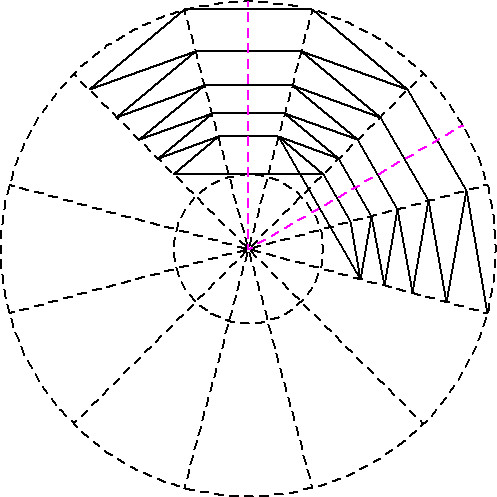
Als nächstes werden die hier zur Verdeutlichung farbig markierten Flächen herauskopiert (siehe nächste zwei Zeichnungen):
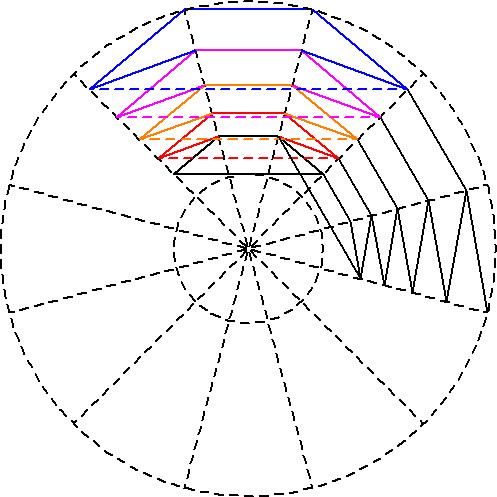
Anschließend werden die Linien in den einzelnen Flächen an der Unterkante gespiegelt und dann die so entstandenen sechseckigen Flächen aneinander geschoben:
Ähnlich verfährt man mit den Flächen, die in der nächsten Zeichnung in Blau- und Grüntönen eingezeichnet sind:
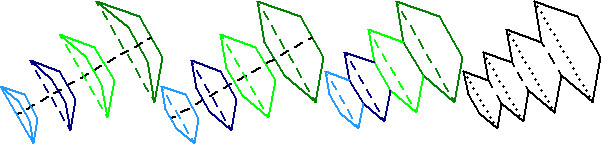
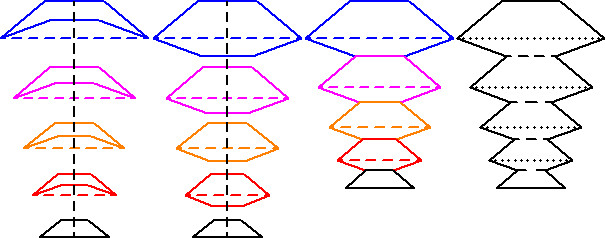
Dann werden die beiden schwarz umrandeten Flächen aus den Zeichnungen oben passend aneinander geschoben:
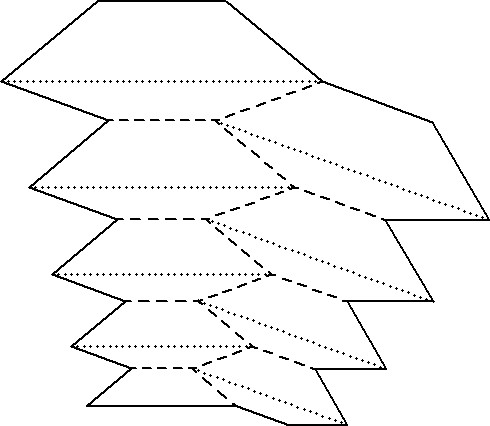
Die gestrichelten Linien werden später wieder nach außen, die punktierten nach innen gefaltet. Dieser Zuschnitt wird dreimal (also N/2 mal) passend aneinander gesetzt, wobei der eine Rand wieder einen zusätzlichen Klebeüberlapp erhält.
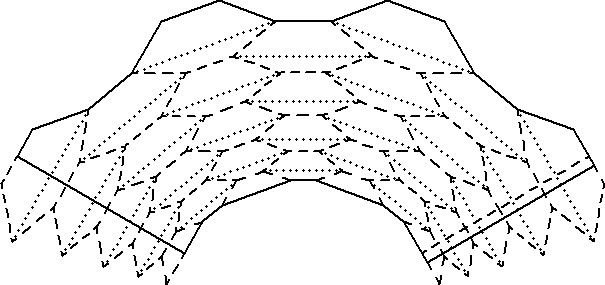
Alle Linien werden mit Lineal und Falzbein genau vorgerillt. Anschließend wird das Blatt zu einem konischen Rohr gerollt und die beiden Kanten werden mit dem Klebeüberlapp verklebt. Dann werden die Falten, an der engeren Seite des Kegelrohrs beginnend, eine nach der anderen von Hand gefaltet. Die ersten Falten sind schwieriger, danach wird es einfacher.
Jetzt ist noch die Frage offen, welchen Winkel β man wählen muss, um die gewünschte maximale Gesamtauszugslänge des Faltenbalgs zu erhalten. Dazu werden hier einige Berechnungen angestellt. Wen nur das Ergebnis interessiert, kann zu den letzten Textabsätzen und Tabellen unten springen.
Die maximale Gesamtlänge eines konischen Faltenbalgs liegt erfahrungsgemäß ungefähr bei einem Drittel der Gesamtlänge L des Papierzuschnitts. Die Gesamtlänge L des Papierzuschnitts ist die Summe der Höhe aller Einzelfalten. Die Höhe der einzelnen Falten nimmt von innen nach außen zu und hängt vom Winkel β ab. Um diese Höhe zu berechnen, werden nacheinander Größen im hellblauen, im schraffierten und dann im gelben Dreieck berechnet:
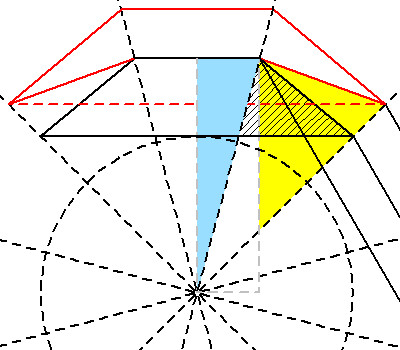
In der nächsten Zeichnung sind die einzelnen Strecken mit Buchstaben bezeichnet:
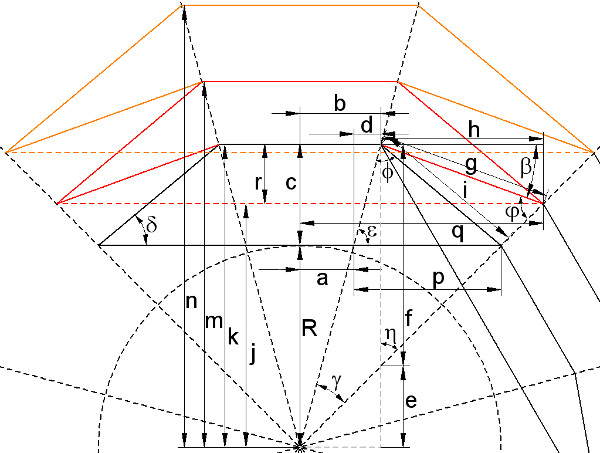
Ab hier steht statt Ri immer nur R. Mit den Winkeln
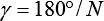 ,
, 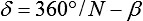 ,
, 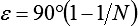 ,
, 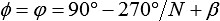 ,
, 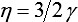
und den Strecken
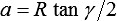
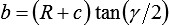
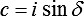 ,
, 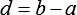
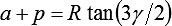 ,
, 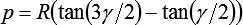
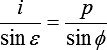
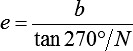
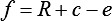 ,
, 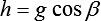 ,
, 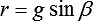
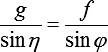
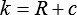
Es ergibt sich k zu:
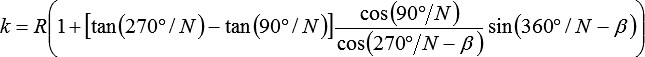
und j zu:
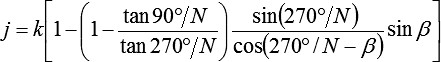
Da aufeinanderfolgende Falten geometrisch ähnlich sind, verhalten sich die Kantenlängen des Papiers einer Falte zum entsprechenden Maß der nächstinneren Falte wie:
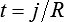
Wegen der geometrischen Ähnlichkeit der Falten gilt für die nächsten Falten:
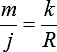
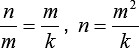
Damit ist die nötige Papierlänge für die i-te Falte des Faltenbalgs:
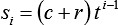
Die Gesamtpapierlänge ist also:
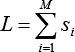
mit der Faltenanzahl M. Die maximale Auszugslänge ist für Faltenbälge, deren beide Enddurchmesser sich deutlich unterscheiden, etwa ein Drittel der Gesamtpapierlänge L.
Kurzanleitung zur Bestimmung des Winkels β
Will man einen konischen Faltenbalg herstellen, legt man zuerst den kleineren Innendurchmesser 2R und den großen Innendurchmesser 2Ra, die Zahl N (N=4 für quadratischen Querschnitt, N=6 für sechseckigen Querschnitt) und die maximale Auszugslänge G fest. Die nötige Gesamtpapierlänge ergibt sich daraus als etwa 3G. Die Anzahl der Falten M legt die maximale Auszugslänge fest und wird von der Wahl des Winkels β bestimmt. Als Anhaltspunkt für die richtige Wahl des Winkels β können die folgenden Tabellen genutzt werden. Die Werte für β liegen immer zwischen 360°/N und 180°/N. Wenn es nicht notwendig ist, den Faltenbalg mit besonders wenigen Falten zu realisieren, sollte die Faltenzahl M so gewählt werden, dass der Winkel β möglichst groß ist. Kleine Winkel β<10° ergeben Faltenbälge mit nur kurzer Auszugslänge. Für β=0 ergibt sich kein sinnvoller Zuschnitt: Die Falten entarten zu einer Ebene. Soll der Außendurchmesser des Faltenbalgs möglichst klein sein, so muss man ein große Zähligkeit N und eine möglichst große Faltenanzahl M wählen.
Die erste Tabelle gibt die Winkel β für Faltenbälge mit quadratischem Querschnitt (N=4) an. Waagerecht ist die Faltenanzahl M, vertikal ist die Gesamtpapierlänge L geteilt durch den kleineren Innenradius R aufgetragen.
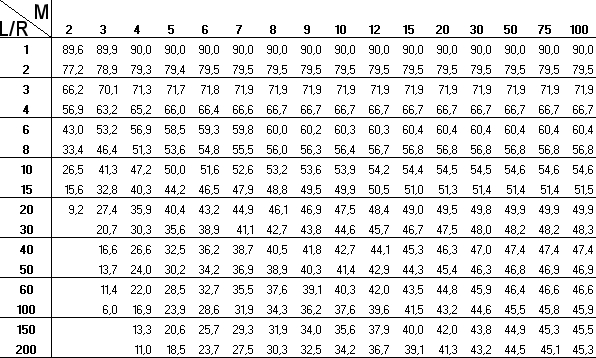
Die zweite Tabelle gibt die Winkel β für Faltenbälge mit sechseckigem Querschnitt (N=6) an. Waagerecht ist die Faltenanzahl M, vertikal ist die Gesamtpapierlänge L geteilt durch den kleineren Innenradius R aufgetragen.
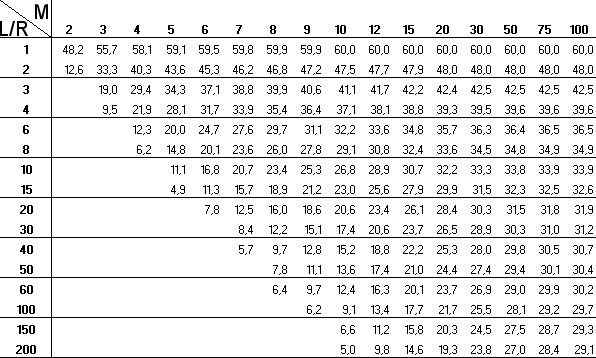
Beispiel: Ein konischer Faltenbalg mit sechseckigem Querschnitt soll an den beiden Enden Innendurchmesser von 60 mm bzw. 100 mm bei einer maximalen Auszugslänge von 80 mm haben.
Damit sind N=6, R=30 mm, Ra=50 mm, G=80 mm. Daraus ergibt sich eine nötige Gesamtpapierlänge von L=3G=240 mm. Der Wert L/R ist 8. Die Faltenanzahl M wird zu M=10 gewählt, damit der Winkel β in der Tabelle oben nicht zu klein wird. Mit diesen Werten M und L/R liest man in der Tabelle für β den Wert β=29,1° ab. Mit der Maus über der Tabelle wird die Ablesung verdeutlicht  . Mit diesem Wert β wird der Zuschnitt wie oben beschrieben gezeichnet. Wenn Sie einen Faltenbalg nach dieser Anleitung gebaut haben, würde ich mich über eine Rückmeldung freuen (Emailadresse steht im Impressum).
. Mit diesem Wert β wird der Zuschnitt wie oben beschrieben gezeichnet. Wenn Sie einen Faltenbalg nach dieser Anleitung gebaut haben, würde ich mich über eine Rückmeldung freuen (Emailadresse steht im Impressum).