Kreisel als Wasserwaage
Auf einer waagerechten Oberfläche bleibt ein rotierender Kreisel auf einer Stelle stehen. Läuft ein Kreisel auf einer Oberfläche nicht seitlich weg, kann man daraus schließen, dass die Oberfläche waagerecht liegt. Damit kann man einen Kreisel wie eine Wasserwaage nutzen.
Wenn sich ein Kreisel auf einer leicht geneigten Oberfläche dreht, dann wandert er senkrecht zur "bergab"-Richtung auf der Oberfläche. Wenn sich der Kreisel andersherum dreht, wandert er in der entgegengesetzten Richtung.
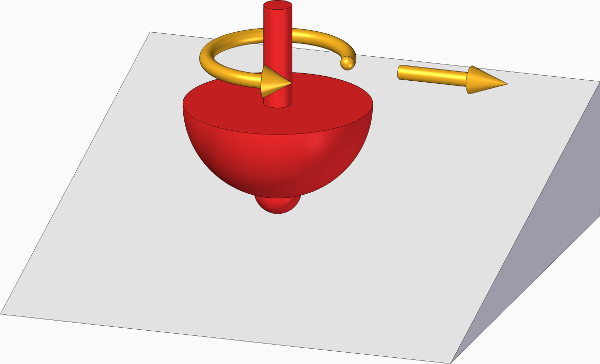
Abb. 1: Ein Kreisel auf einer geneigten Ebene; der eine Pfeil gibt die Drehrichtung des Kreisels an, der andere die Wanderrichtung des Kreisels
Die Ursache ist, dass die Kreiselspitze nie ganz spitz, sondern etwas gerundet ist. Dadurch liegt der Punkt auf dem der Kreisel steht nur bei einer waagerechten Fläche genau auf der Rotationsachse des Kreisels. Bei einer geneigten Fläche liegt der Aufstandspunkt des Kreisels in einem Abstand r zur Drehachse. Dadurch rollt der Kreisel auf einem kleinen Kreis um seine Drehachse ab und damit rollt er bei jeder Umdrehung etwas weiter.
Aus der Wandergeschwindigkeit v lässt sich der Neigungswinkel a der Oberfläche berechnen. Die Wandergeschwindigkeit v hängt vom Neigungswinkel der Oberfläche, von der Drehzahl n des Kreisels und vom Radius RSpitze der Kreiselspitze ab.
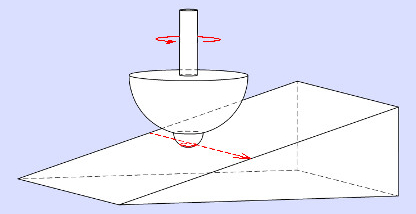
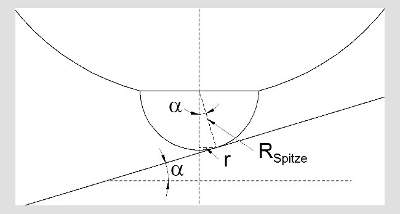
Abb. 2: Der Kreisel rollt auf einem kleinen Kreis um die Spitze des Kreisels ab.
Bei jeder Umdrehung des Kreisels rollt er auf der Oberfläche die Länge des Umfangs Ur eines Kreises mit dem Radius r weiter:
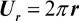
mit
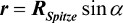
Die Wandergeschwindigkeit v des Kreisels ist:
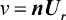
Damit ist der Neigungswinkel a der Oberfläche:
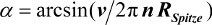
Beispiel: Ein Kreisel mit einem Spitzenradius von 1 mm dreht sich mit 20 Umdrehungen/s und wandert mit 10 mm/s über eine Oberfläche. Diese hat damit einen Neigungswinkel von:
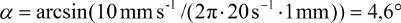
Da die Messung der Drehzahl des Kreisels und des Radius der Kreiselspitze schwierig sind, begnügt man sich besser damit, den Kreisel nur als Wasserwaage und nicht zur Messung des Oberlfächenneigungswinkels zu nutzen. Oder man legt einfach eine Murmel auf die Fläche: Wenn sie nicht rollt, ist die Fläche eben.
